This material is one of the perspectives on the F1 (113) Applied Mathematics specialty, discussing its characteristics and focus. I hope it will help future applicants choose the bright side of the path to IT specialties, which undoubtedly goes through mathematics. Part of the text was recorded during a meeting with the Head of the Department of Mathematical Modeling and Intelligent Computing in Engineering, which took place during the presentation of the educational program “Computer and Mathematical Modeling”.

Vodka Oleksiy Oleksandrovych – Head of the Department of Mathematical Modeling and Intellectual Computing in Engineering, Candidate of Technical Sciences, Associate Professor, Laureate of the President of Ukraine Award for Young Scientists.

Department of Mathematical Modeling and Intelligent Computing in Engineering – a graduating department in the specialties F3 (122) “Computer Science” and F1 (113) “Applied Mathematics”, has been training specialists in the field of mathematical modeling since 1930, and since 1999 has been training specialists in computer science, the department is part of the Educational and Scientific Institute of Computer Modeling, Applied Physics and Mathematics (ICM).

Hello everyone,

F1 (113) Applied Mathematics – what is it?

Let’s try to determine what applied mathematics is and what it is needed for. If you open Wikipedia, the definition of Applied Mathematics is formulated as follows:

Applied mathematics means the application of mathematical methods in various fields: physics, engineering, medicine, biology, finance, business, computer science, etc. Today, applied mathematics is not about theorems, but about the application of mathematical methods to various models in various applied fields.

Applied mathematics, as a specialty, works on the formulation of problems and the use of models. The main task of an applied mathematician, as a specialist, is to create, using applied knowledge, mathematical models for studying the world around us, or any applied field.

What exactly is studied in our educational program in the specialty F1 (113) Applied Mathematics? In which fields are mathematical models created and applied?

Specialty and educational program

Let’s first understand what a specialty is, and what an educational program is. Each specialty has an educational standard that determines 50% of the mandatory educational components (subjects). The other 50% is determined by the educational program and free choice disciplines (elective disciplines). There can be several educational programs for a specialty. For example, there are two of them at NTU “KhPI”. Each of the educational programs has its own direction (focus). The educational program that we will talk about further is called “Computer and Mathematical Modeling”. As for elective disciplines, they make up 25% of the total number of subjects according to the requirements of the Ministry of Education and Science of Ukraine. These are the disciplines that you can choose, specifying and expanding your profile in any direction. This can be data analysis, special modeling methods, specific programming, etc.

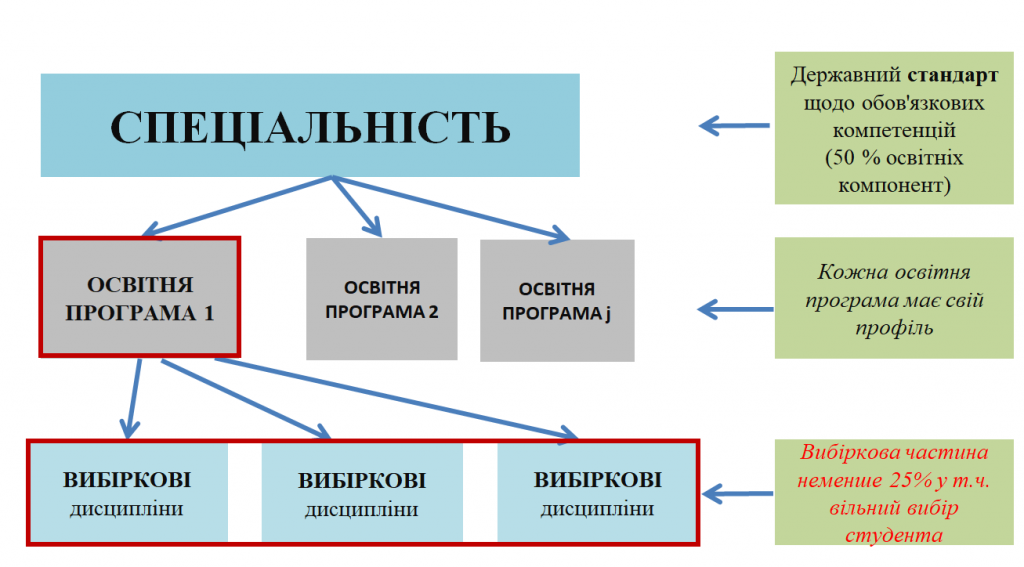
Focus of the educational program. What exactly is the educational program “Computer and Mathematical Modeling” presented by our department aimed at?
Well, first of all, it must be said that this is a program for training bachelors in applied mathematics who are able to formulate, solve and generalize practical problems using fundamental and special applied methods of mathematics and IT for modeling, analyzing and processing processes and phenomena in engineering and information systems.

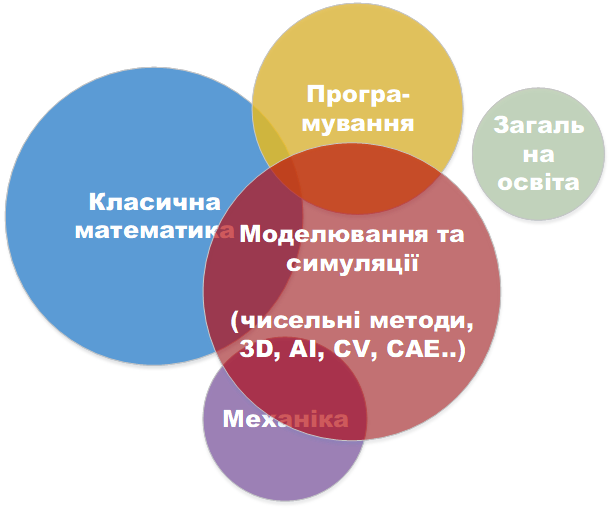
If we depict this in the form of a diagram, we see classical mathematics on it as a necessary component and the main tool. However, modern mathematics cannot be applied with a pencil and a piece of paper. To do this, you need to perform calculations – give instructions to the computer how and what to calculate, you need to create a program that implements mathematical ideas and methods. This means that a large part of a mathematician’s work is program development and programming. Combining mathematics and programming, you can conduct numerical simulations and modeling, build models that are used on a computer. This includes 3D modeling, modeling using engineering packages, computer vision tasks for recognizing objects that need to be worked with, and artificial intelligence, which is very popular today. One of the areas of application of our knowledge is mechanical engineering, which is associated with the design of structures of varying complexity. We will talk about this later.

While studying at the university, students also receive mandatory classical training, which includes economic disciplines, languages, history, philosophy, etc.

There are two groups of subjects in our educational program.
Subjects that are typical for the entire specialty F1 (113) Applied Mathematics:

• Programming (C++, C#, Python…)
• Mathematical analysis, Analytical geometry
• Linear algebra, logic, special sections
• Differential equations, series
• Probability theory, statistics
• Data structures and databases
• Numerical methods, computer algebra (Matlab, Maple)

Subjects of our educational program F1 “Computer and mathematical modeling”, which complement the previous ones:

• Computer numerical simulations
• 3D modeling
• Structural analysis
• Analytical mechanics
• Stochastic processes
• Discrete and nonlinear dynamic processes
• Signal and image processing
• Artificial intelligence
• Optimization and control
• Data mining

All these subjects can be applied to different areas of application.

Modeling and applied mathematics

First of all, when talking about modeling, you need to understand what it is? When I ask my students what modeling is? They all answer together that modeling is the process of creating models. If we turn again to our beloved Wikipedia, we can see the following definition:

And when you ask what a model is? Here opinions differ. It is clear that we are talking about creating models using computers, but, still, the ways of building models on a computer are very different. But we all subconsciously realize that a model is a simplified representation of reality: a phenomenon or situation that can be controlled or analyzed for its behavior, etc. So, returning to modeling, what is it? Again, Wikipedia identifies many types of modeling:

Among the variety of modeling types, we need to choose those that, on the one hand, correspond to the profile of the department, so “Historical” or “Pedagogical” modeling is eliminated, and, on the other hand, computer science methods (software development, algorithm theory, data structures, computational methods) are used to create models using a computer. So, from the huge list, four areas will remain:

• Mathematical modeling;
• Computer modeling;
• 3D modeling;
• Data-based modeling.

What is it? mathematical modeling? This is classical modeling, when knowledge of mathematics, higher mathematics or some branches of mathematics such as differential equations, integral calculus, etc. are used to solve specific problems.

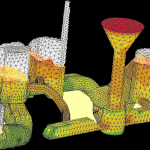
Computer modeling is when a process is described in a computer using equations. But there is a peculiarity here, the computer itself, under the control of the user, composes the equations itself, and solves them itself. Typically, this is a very complex computational procedure that requires a large amount of RAM and computing cores. Sometimes supercomputers are needed to solve such problems.

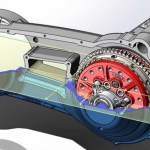
The next is 3D modeling – this is when a computer is used to create 3D models of an object. 3D modeling is an integral part of using 3D printers. That is, first you need to create a 3D model, and then print it on the printer. By the way, we have a 3D printer at the department and students can join projects using a 3D printer if they wish.

And finally, data-based modeling. Let’s analyze this type of modeling using the example of a store. You probably all have a card from the store where you buy products? Why do you think the store should give it to you? For the sake of a discount? In fact, the store is trying to build a buyer model based on the data about you that it collects. When you apply for a card, the store signs an agreement with you that the store gives you the card, and you leave it your personal data (age, gender, marital status) and data about your purchases. Then, using this card, the store collects your needs in a personalized way: the products you buy, how often you buy them, which ones you buy most often, etc. Then the store analyzes this information for a better understanding of buyer behavior, how many and which products need to be in stock to satisfy demand.

Returning to data-driven modeling as a new method of creating models, it is impossible not to mention the advantages of this method compared to classical approaches. Classical approaches use the idea that you need to write some equations, make some predictions or determine the probability of an event. This is a very complex process, and sometimes it is much faster to have a network of sensors that monitor the state of the system, and, thus, can give predictions. Such a network of sensors is sometimes more practical and understandable and gives a more accurate prediction than using classical mathematical models.

All these types of modeling can be applied to various areas of future activity, or areas of application of knowledge. For example, the following:

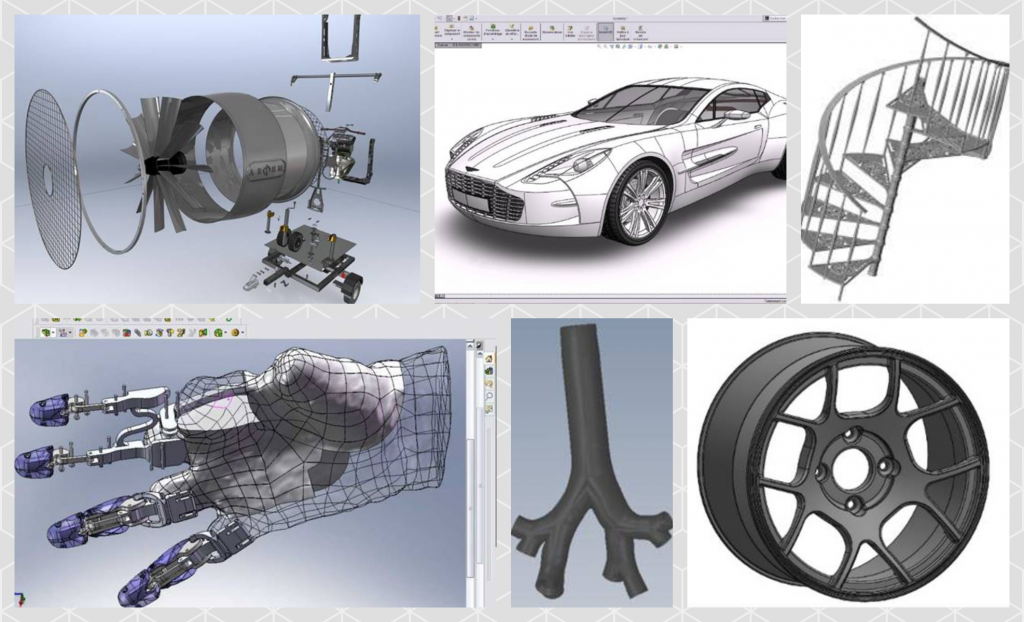
Creating 3D models

Creating detailed 3D models, which may include models of turbines, robotic systems, biomechanical systems, classical mechanical models, i.e. models of engineering objects. These models are often used to conduct computer simulations.

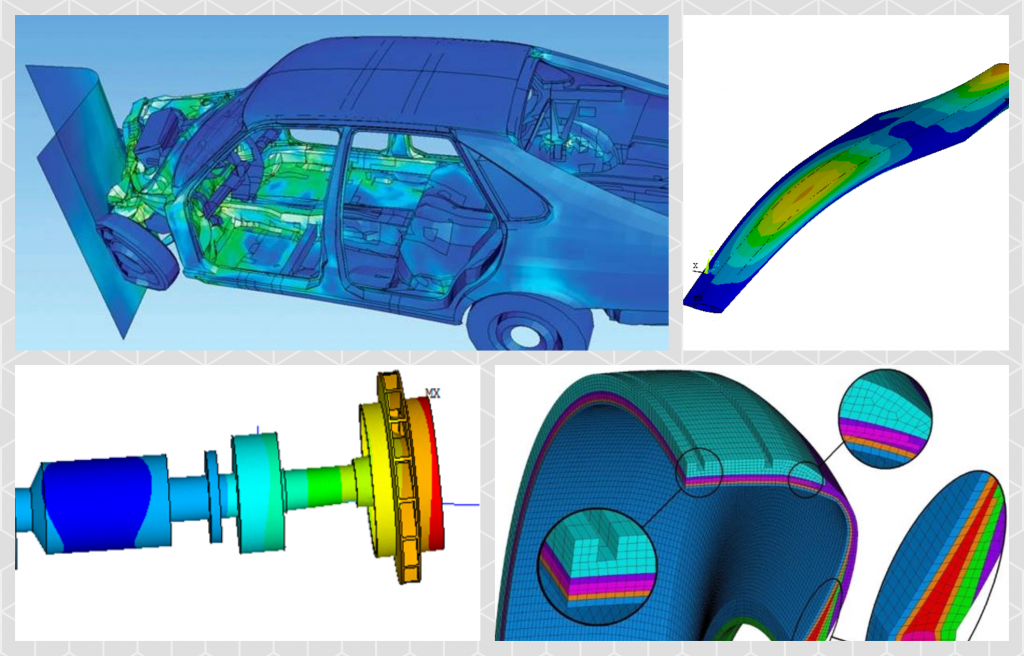
Computer simulations

It is computer simulations that allow you to conduct numerous experiments on a computer and significantly reduce expensive real experiments. For example, in order to confirm the safety of a car, a test is usually conducted in which the car is crashed into a wall at a speed of about 60 km/h and the consequences are recorded. But if you need to do a series of such tests, correcting the design, it is very expensive. An alternative to such experiments is computer simulation. To do this, a model of the design is created, in this case a car, and predict how this design will behave when it hits a wall. Identifying weak points in the design and strengthening and improving it, you can carry out such a simulation the required number of times. Thus, you can ensure the safety of the design, and then conduct, for example, one real crash test and confirm that everything is exactly as it was modeled on the computer.
Computer simulation can create models of various designs. These can be models of turbine blades, car tires, turbogenerator rotors, etc.

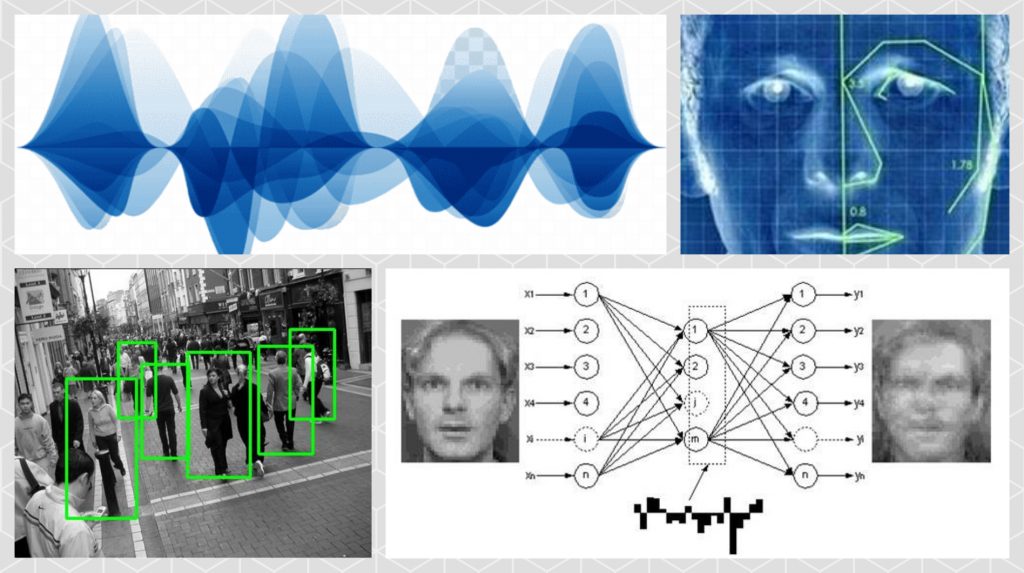
Data analysis, diagnostics and recognition

If you need to develop a model of something, and there are no classical mathematical models, you can process a large amount of data (photographs, videos, or some tabular data recorded from sensors) and build a forecast of the system’s behavior. For this purpose, data analysis methods, artificial intelligence methods, pattern recognition methods and computer vision can be used. In this case, mathematical algorithms are used for data processing, which allow us to use our models in applied problems.

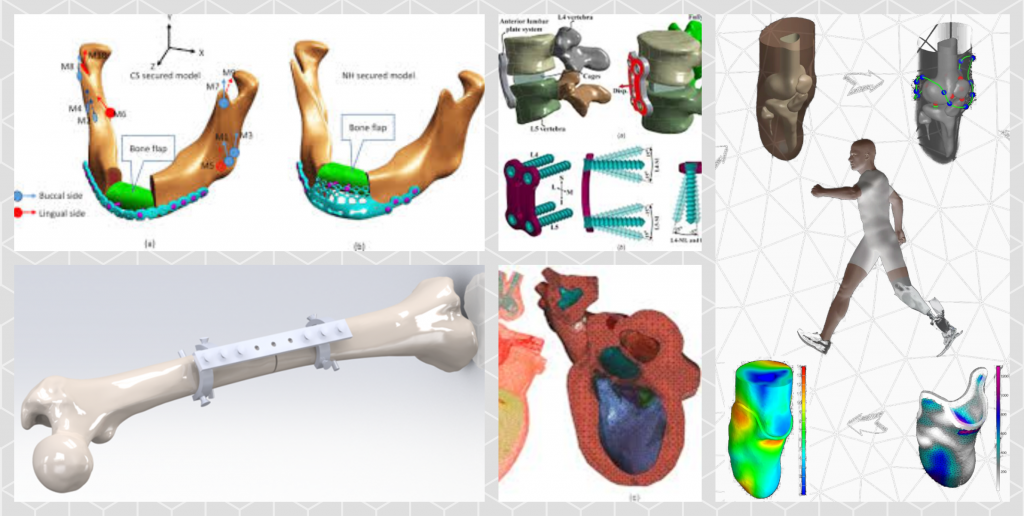
Modeling of biomaterials and systems (biomechanics)

Another direction is the modeling of biomaterials and biosystems. A person is also a mechanical structure, but a specific one. He has blood vessels, muscles, bones. And the behavior of these components can also be predicted. In the event of fractures or injuries, it is necessary to calculate special fixators that will accelerate recovery. Continuing the example with a bone fracture, it is clear that doctors try to fix the fixator as firmly as possible on the bone when it is fractured in several places. How to determine the required number of fixators on the bone? The patient wants to receive as little additional damage as possible. How to find a balance? Mathematical modeling also comes to the rescue here, which allows doctors to provide the necessary recommendations. However, such “living” materials have very complex nonlinear behavior, so building such a model is very difficult.

Similar modeling can be done to study vascular mechanics and the effects of atherosclerosis. Similar problems arise when installing dental implants. They must withstand the load of chewing and not break when hard food hits them. They must also withstand millions of cycles of chewing. Such modeling is also possible thanks to the methods taught and provides the patient with individualized predictions.

Benefits of studying and features of the “Computer and Mathematical Modeling” program

In order for you to better understand what benefits you get by choosing this educational program, we have prepared a small list for you:

The team teachers

One of our competitive advantages is the team of teachers who will work with you. The team includes both experienced professors and young practicing teachers who can communicate with you in the same language, understand modern slang and will be able to easily establish contact with you. You can get to know each one better on the relevant page of our website.

 Project-based learning

One of the features of our educational program is the project-based learning. Students starting from the 3rd year work in teams on their own development (project). Such projects are coordinated by representatives of private companies, our partners. They are created in the areas of data analysis, structural modeling, software development. Students are invited to develop some part of a real working project under the guidance of specialists working in IT or related fields. Students can go through all stages of a team project from setting a task to designing and presenting results. This allows students to develop not only professional skills, but also communication skills.

 International Relations and Academic Mobility

The Department of Mathematical Modeling and Intelligent Computing in Engineering is known with its international ties with scientific partners from different countries. Not only scientific cooperation is carried out with all partners, which allows the department to ensure academic mobility. Students, postgraduate students and teachers can go to another higher education institution for a certain period of time for study and internship.
In different years, groups of students and teachers went for practice to universities in Germany. As part of international cooperation, the Leonard Euler scholarship for students was launched in 2001. And every year 3-5 students receive this scholarship. Recently, the number of such programs has significantly increased.

 Presence of history

Our department has been training specialists in mathematical modeling since 1930. A powerful scientific school has been created. And the execution of diploma theses using computer technology began back in 1969, as one of the first departments at the university. On the first huge computers that existed at that time, which could occupy an entire floor, students of our department created programs that used the developed mathematical models to calculate technical systems.
All teachers of the department are engaged in scientific work, conduct scientific research, present them at international conferences, participate in international grants, and participate in international cooperation.

Summary

F1 (113) Applied mathematics is a fundamental education, a great history, this year the Department of Mathematical Modeling and Intellectual Computing in Engineering turns 93, so we know exactly what applied mathematics, programming, mathematical modeling are, and what it should be and how to teach it.

Features of this year’s admission

Features of this year’s admission are the national multi-subject test (NMT). It includes a new version of the external assessment, which combines three subjects. Another innovation this year is a motivation letter, which is mandatory for admission to F1 (113) Applied Mathematics. In order to enroll on a budget, you need to pass the NMT or have external assessment from previous years, and write a motivation letter. If you want to enroll on a contract, you only need a motivation letter. The cost of tuition is 18 thousand hryvnias per year, payment in installments is possible.

That’s all I wanted to tell you about F1 (113) Applied Mathematics and our educational program “Computer and Mathematical Modeling” at the Department of Mathematical Modeling and Intelligent Computing in Engineering.

Thank you for your attention!

Other useful links:

• More details on the specialty F1 (113) Applied Mathematics: “Computer and Mathematical Modeling”
• More about applied mathematics on the PCM website
• Website of the Department of Mathematical Modeling and Intelligent Computing in Engineering
• Our Telegram chat for F1 (113) specialties. And for F3 (122) specialties. Live communication and answers to all questions
• Video version of this meeting: